Testing the effectiveness of Get-Random

An ongoing argument I’ve seen in the PowerShell community is regarding the effectiveness of random numbers generated by the Get-Random cmdlet. Those who claim that Get-Random does not produce cryptographically strong random data advocate using the System.Security.Cryptography.RNGCryptoServiceProvider .NET class as an alternative.

Well, which one is stronger? The answer to that question depends on how one defines “cryptographically strong.” For the sake of simplicity, we will define “cryptographically strong” as data that is sufficiently random (i.e. high entropy) and is unpredictable. Let’s start by discussing randomness.

Full disclosure: I am neither a cryptographer nor a mathematician, therefore, I am far from qualified to speak with sufficient authority on how to implement a proper pseudorandom number generator. Apparently, this is even a hard problem for mathematicians and cryptographers on government standards boards.

Randomness

How can we tell how “random” something is? It’s actually fairly easy to visualize by looking at a histogram of the frequency of which each byte in a sequence occurs. For example, here’s a frequency diagram of an uncompressed kernel32.dll vs. a frequency diagram of kernel32.dll as a compressed and encrypted zip file.

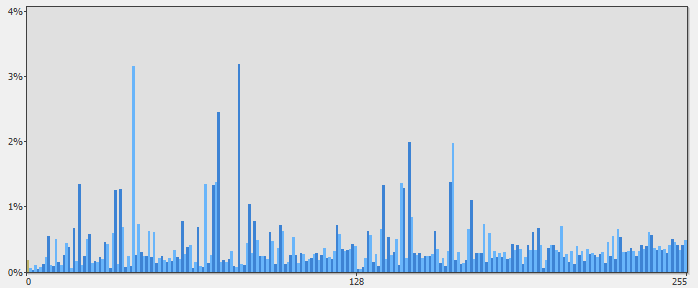
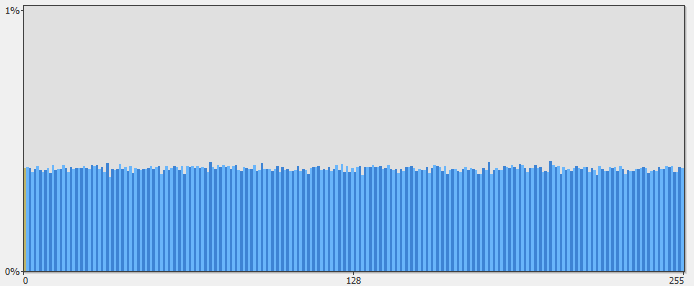
The X-axis indicates a byte value 0-255 and the Y-axis indicates the percentage of occurrences for each byte. You can see that the frequency diagram of the uncompressed kernel32.dll has many peaks and valleys, whereas, compared to the compressed and encrypted version, the distributions of bytes has “flattened”. The aggregate distribution of frequencies refers to the randomness of the data. This concept is known as entropy.

Now, if we’re going to test the randomness of data, eyeballing it will not suffice. We need a way to quantify the randomness of a dataset. Fortunately, we have the following handy formula:

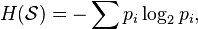
For those who haven’t dealt with this kind of math for a while, don’t let this equation scare you. It simply represents the sum of each byte frequency percentage scaled to a value between 0 (no entropy – i.e. a sequence consisting of a single byte) and 8 (maximum entropy – i.e. purely random data). This equation can be easily converted into a function in PowerShell.

function Get-Entropy
{
    Param (
        [Parameter(Mandatory = $True)]
        [ValidateNotNullOrEmpty()]
        [Byte[]]
        $Bytes
   )

   $FrequencyTable = @{}
   foreach ($Byte in $Bytes) {
       $FrequencyTable[$Byte]++
   }
   $Entropy = 0.0

   foreach ($Byte in 0..255)
   {
       $ByteProbability = ([Double]$FrequencyTable[[Byte]$Byte])/$Bytes.Length
       if ($ByteProbability -gt 0)
       {
           $Entropy += -$ByteProbability * [Math]::Log($ByteProbability, 2)
       }
   }
   $Entropy
}

Get-Entropy takes a byte array and calculates its entropy.

Now, here’s a simple function that generates a byte array using either Get-Random or by using the RNGCryptoServiceProvider class.

function Get-RandomByte
{
    Param (
        [Parameter(Mandatory = $True)]
        [UInt32]
        $Length,
        [Parameter(Mandatory = $True)]
        [ValidateSet('GetRandom', 'CryptoRNG')]
        [String]
        $Method
    )

    $RandomBytes = New-Object Byte[]($Length)

    switch ($Method)
    {
        'GetRandom' {
            foreach ($i in 0..($Length - 1))
            {
                $RandomBytes[$i] = Get-Random -Minimum 0 -Maximum 256
            }
         }
         'CryptoRNG' {
             $RNG = [Security.Cryptography.RNGCryptoServiceProvider]::Create()
             $RNG.GetBytes($RandomBytes)
         }
    }
    $RandomBytes
}

So now we have the components necessary to put Get-Random and RNGCryptoServiceProvider to the test. To see which method generates data with a higher entropy, we’ll generate 4096 random bytes 100 times, compute the average entropy, and then compare the two averages. If one method has an entropy that deviates greatly from the other, then we will have a clear winner in terms of randomness.

Here is our test code:

# Generate 0x1000 random bytes 100 times using

# Get-Random and RNGCryptoServiceProvider.

$Results = 1..100 | % {
    $Length = 0x1000
    $GetRandomBytes = Get-RandomByte -Length $Length -Method GetRandom
    $CryptoRNGBytes = Get-RandomByte -Length $Length -Method CryptoRNG
    $Randomness = @{
        GetRandomEntropy = Get-Entropy -Bytes $GetRandomBytes
        CryptoRNGEntropy = Get-Entropy -Bytes $CryptoRNGBytes
    }
    New-Object PSObject -Property $Randomness
}

$GetRandomAverage = $Results | measure -Average -Property GetRandomEntropy
$CryptoRngAverage = $Results | measure -Average -Property CryptoRNGEntropy

$AverageEntropyResults = New-Object PSObject -Property @{
    GetRandomAverageEntropy = $GetRandomAverage.Average
    CryptoRngAverage = $CryptoRngAverage.Average
}

So who came out on top??? No one!

$AverageEntropyResults | Format-Table -AutoSize
CryptoRngAverage GetRandomAverageEntropy
---------------- -----------------------
7.95390371502568         7.9547142068139

The entropy generated by Get-Random and RNGCryptoServiceProvider are both close enough to purely random data (entropy = 8) that they are both excellent candidates for generating random data.

Predictability

Predictability refers to the likelihood that one would be able to guess the next number in a sequence of “random” numbers. Random number generators require a seed value – a number used for the initialization of a random sequence. How the seed value is chosen is extremely important as it has a direct impact on the predictability of a random sequence.

If an identical seed value is chosen for two or more random sequences, the sequences will be identical. For example, try running Get-Random using a fixed seed:

PS> 0..255 | Get-Random -Count 10 -SetSeed 1
216
161
109
239
111
129
71
26
113
249

PS> 0..255 | Get-Random -Count 10 -SetSeed 1
216
161
109
239
111
129
71
26
113
249

When a seed value is not provided to Get-Random, the system tick count – the number of milliseconds elapsed since the system started is used as a seed. Executing Get-Random without a seed is equivalent to executing:

Get-Random -SetSeed ([Environment]::TickCount)

Now, the tick count is a 32-bit number which means that there are 4,294,967,295 possible seed values. Such a massive number ought to produce sufficiently unpredictable sequences, right? No.

Let’s envision a scenario where we use Get-Random to generate random passwords and the script is scheduled to run five minutes after system startup. What’s the likelihood that the script generates the random password at the same tick count as the last time a password was generated? It probably unlikely that you would hit the exact number of milliseconds but for a fast computer, it’s probably likely that you are guaranteed that a set of seeds within a specific time interval will be used. Let’s say that we determined that the script was likely to execute within 2000 milliseconds (2 seconds) of the last time the script executed. That means that there is only a maximum of 2000 possible passwords that one would need to guess. For a determined adversary intent on obtaining a critical password, this is not a far-fetched task.

RNGCryptoServiceProvider, on the other hand is designed to use an unpredictable seed value unlike the predictable system tick count used in Get-Random. This means that regardless of the time of day, an unpredictable, random sequence will be generated.

Conclusion

So who wins the Cryptography Strongman contest?

The winner is RNGCryptoServiceProvider based on its randomness and unpredictability.

What’s the lesson in all this? If you’re using a random number generator as the basis for providing security, you must use a cryptographically secure random number generator. For quick and dirty scripts that have nothing to do with security, Get-Random is just fine.